Salah satu Struktur Data yang teramat penting adalah Array
atau Larik.
Array dapat didefinisikan sebagai suatu himpunan hingga elemen, terurut dan homogen. Atau Dapat didefinisikan juga sebagai pemesanan alokasi memory sementara pada komputer.
Terurut : Dapat diartikan bahwa elemen tersebut dapat diidentifikasi sebagai elemen pertama, elemen kedua dan seterusnya sampai elemen ke-n.
Array dapat didefinisikan sebagai suatu himpunan hingga elemen, terurut dan homogen. Atau Dapat didefinisikan juga sebagai pemesanan alokasi memory sementara pada komputer.
Terurut : Dapat diartikan bahwa elemen tersebut dapat diidentifikasi sebagai elemen pertama, elemen kedua dan seterusnya sampai elemen ke-n.
Homogen : Adalah bahwa setiap elemen dari sebuah Array tertentu haruslah mempunyai type
data yang sama. Sebuah Array dapat mempunyai elemen yang semuanya berupa integer atau dapat pula
seluruhnya berupa character atau String bahkan dapat pula terjadi suatu Array
mempunyai elemen berupa Array pula.
Karakteristik Array :
1. Mempunyai batasan dari pemesanan alokasi
memory (Bersifat Statis)
2. Mempunyai Type Data Sama
(Bersifat Homogen)
3. Dapat Diakses Secara Acak
Karakteristik Array :
1. Mempunyai batasan dari pemesanan alokasi
memory (Bersifat Statis)
2. Mempunyai Type Data Sama
(Bersifat Homogen)
3. Dapat Diakses Secara Acak
Adapaun jenis Array yang akan dipelajari adalah :
1. Array
Dimensi Satu (One Dimensional)
2. Array
Dimensi Dua (Two Dimensional)
3. Array Dimensi Banyak (Multi Dimensional)
1. ARRAY DIMENSI SATU
(One Dimensional)
Deklarasi
: Var A : Array[1..N] Of Type Data;
Penggambaran
secara Logika :
Harga minimum dari subskrip suatu Array disebut sebagai
batas bawah atau lower bound (L), sedangkan harga maksimumnya disebut batas
atas atau upper bound (U).
PEMETAAN ARRAY DIMENSI SATU KE STORAGE
Mapping Storage Array Dimensi Satu
Rumus : @A[I] = B + {U - 1} * L
Dimana @A[I] : Posisi Array Yg Dicari
B : Posisi Awal Array di Memory Komp.
U : Subkrip atau Indeks Atas Array
L : Besar Memory dari St. Type Data
Rumus menentukan jumlah elemen dalam Array :
Jumlah Elemen :
n
p (Ui – Li)
i=1
p = Pi (Perkalian dari statemen sebelumnya)
{Dosen membuat contoh aplikasi mapping
array dimensi satu}
Mapping Storage Array Dimensi Satu
Rumus : @A[I] = B + {U - 1} * L
Dimana @A[I] : Posisi Array Yg Dicari
B : Posisi Awal Array di Memory Komp.
U : Subkrip atau Indeks Atas Array
L : Besar Memory dari St. Type Data
Rumus menentukan jumlah elemen dalam Array :
Jumlah Elemen :
n
p (Ui – Li)
i=1
p = Pi (Perkalian dari statemen sebelumnya)
{Dosen membuat contoh aplikasi mapping
array dimensi satu}
2. ARRAY DIMENSI DUA
(Two Dimensional)
B.U : Var A : Array[1..N,1..M] Of Type Data;
Sering digunakan dalam menterjemahkan matriks pada pemrograman.
Mis : Var A : Array[1..3,1..4] Of Integer;
Terbagi Dua cara pandang (representasi) yang berbeda :
1. Secara Kolom Per Kolom (Coloumn Major Oder)
@M[i,j] = @M[1,1] + {(j - 1) * K + (i - 1)} * L
B.U : Var A : Array[1..N,1..M] Of Type Data;
Sering digunakan dalam menterjemahkan matriks pada pemrograman.
Mis : Var A : Array[1..3,1..4] Of Integer;
Terbagi Dua cara pandang (representasi) yang berbeda :
1. Secara Kolom Per Kolom (Coloumn Major Oder)
@M[i,j] = @M[1,1] + {(j - 1) * K + (i - 1)} * L
2. Secara Baris Per Baris (Row Major Order)
@M[i,j] = @M[1,1] + {(i - 1) * N + (j - 1)} * L
Ket : I = Baris, j = kolom, L = panjang elemen
K = Banyaknya kolom
N = Banyaknya baris
@M[i,j] = @M[1,1] + {(i - 1) * N + (j - 1)} * L
Ket : I = Baris, j = kolom, L = panjang elemen
K = Banyaknya kolom
N = Banyaknya baris
3. ARRAY DIMENSI TIGA (Three
Dimensional) dan Dimensi Banyak
(Multidimensional)
B.U : Var A : Array[1..N,1..M,1..P,1..R,…] Of Type Data;
Pada dasarnya hanya pengembangan dari array dimensi tiga, yaitu :
@M[n,m,p,r,….] = @M[1,1,1,1,….] + {(n-1)*(Ui-Li+1)+(m-1)*(Ui-Li+1)+ (p-1)* (Ui - Li + 1)+……} * L
B.U : Var A : Array[1..N,1..M,1..P,1..R,…] Of Type Data;
Pada dasarnya hanya pengembangan dari array dimensi tiga, yaitu :
@M[n,m,p,r,….] = @M[1,1,1,1,….] + {(n-1)*(Ui-Li+1)+(m-1)*(Ui-Li+1)+ (p-1)* (Ui - Li + 1)+……} * L
TRINGULAR ARRAY (ARRAY SEGITIGA)
Beberapa aspek pelinieran suatu Array yang harus ditinjau adalah Tringular Array. Tringular Array dapat merupakan Upper Tringular (seluruh elemen di bawah diagonal utama = 0), ataupun Lower Tringular (seluruh elemen di atas diagonal utama = 0).
Dalam Array Lower Tringular dengan N baris, jumlah maksimum elemen <> 0 pada baris ke-I adalah = I, karenanya total elemen <>0, tidak lebih dari
N
SIGMA I = N(N+1)/2
I=1
Beberapa aspek pelinieran suatu Array yang harus ditinjau adalah Tringular Array. Tringular Array dapat merupakan Upper Tringular (seluruh elemen di bawah diagonal utama = 0), ataupun Lower Tringular (seluruh elemen di atas diagonal utama = 0).
Dalam Array Lower Tringular dengan N baris, jumlah maksimum elemen <> 0 pada baris ke-I adalah = I, karenanya total elemen <>0, tidak lebih dari
N
SIGMA I = N(N+1)/2
I=1
Gambar (a) Upper Triangular Array
(b)
Lower Triangular Array
Contoh berikut.
SPARSE ARRAY (ARRAY JARANG).
Suatu
Array yang sangat banyak elemen nol-nya, dikenal sebagai Sparse Array,
contohnya adalah Array A pada Gambar berikut :








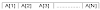

0 Comments